yeah i’ve used a bunch of languages both personally and professionally and i’m not particularly in love with any of them.
javascript, typescript, objective c, swift, java, kotlin, python, c#, lua, perl are the ones i’ve made anything in.
they’re all varying degrees of bad (some in pretty novel ways). java might be the worst, though.
i get a lot of entertainment when a language encourages you to do complicated things for hardly any benefit, so i got a real kick out of the type system in typescript.
this is how i did strongly typed components in my wumpus game. making new constructors for components in that C object automatically generates all the types for you. and it took me like an hour of reading the typescript docs and pondering to come up with it. hilarious!
usage looks something like this:
where those strings only accept actual component names, and then within the block or collection all the objects are typed correctly (have the components i’ve verified they have)
i used to be a big proponent of strongly typed languages but having worked enough in untyped languages it’s not as big a deal as people make it, or maybe my brain is just broken in the right ways for it to be a non-issue.
i do, however, think null safety is one of the nicer things new languages are doing.
yeah theres a few things about go that are generally annoying, local dependencies being one of them, but overall i think its pretty great at what its designed to do (limiting language features just enough to prevent business coders from fucking your enterprise codebase beyond maintainability)
I should say, like, I don’t necessarily think there’s anything wrong with beginners writing pseudocode, that seems like fine for anyone to do I think and we’re all beginners in some sense…I guess just like, in terms of presenting programming ideas to others on a web forum, I worry it might be easy to express things in ways that might be less accessible than if they were phrased in a “practical language” the readers were already familiar with, unless you generally knew what their background was to some extent.…although I guess that’s basically why I started this thread, so maybe my worries in my last post make less sense now that we do have a better idea of what people’s background is. 
I feel fairly similar, yeah. Javascript has gained a lot of nicer features over the years—I feel like it’s easier to tolerate today than it was back in the 00s, although it still has lots of little bugbears that kinda annoy me when I do have to write it (depends a lot on what I’m trying to do though…I wish Web Audio was better although I guess that’s not exactly JS per se…). I use Ruby as a shell scripting replacement more than anything else these days too, although I feel like it’s underused for game development kinda just because there’s not a popular modern engine that uses it. I will say that I’ve had good results both embedding a Ruby interpreter and using mruby in the context of mainly-C++-based SDL projects and that sort of thing…so I think there is at least potential to have a modern engine that uses it. ^^ And there’s always VX Ace of course, you can make any game in that as long as you’re okay with 640x480. ;D
Also, what popular language today isn’t an ALGOL descendent in some sense? I guess maybe that was your point. You could argue that LISPs aren’t, I guess, at least sort of.
That’s interesting…I like Haskell, I don’t know if I’m quite as into Rust…I think I’m more of a C++ person than a Rust person. They suit different temperaments I think—Rust has maybe a more “one way to do it” kinda vibe like Python strives for, whereas C++ is more trusting of the programmer and lets you do things your way. I’ve heard people argue passionately in favor of both sides. One thing I will say is that C++ does allow you to strictly enforce type and memory safety as widely as Rust does, it’s just easier to sideskirt and more “opt-in” in various ways; Rust fans tend to feel like that’s a liability it seems like, but I generally prefer it, especially for things like games or audio software etc. where the design of the program is very fluid and you want a lot of freedom to experiment as you’re working and so on. C++ always gives you an easy escape valve, and that makes it easy to try random things out as you go without having to compromise the larger design. (I also love how expressive C++'s type system is; I can’t say I’ve felt the same way about Rust although maybe I just haven’t spent enough time with it.)
I actually like null, often I feel like it’s very natural although sometimes I think its presence in an API could be more carefully thought-out. I think it tends to fit in better in dynamic languages than static ones (I like Ruby’s treatment of it in its stdlib for example). One thing I think it’s nice to remember about it in any case is that you only really have to check for it at the edges of your program, where things come in from the outside world, because that’s where everything unknowable at runtime lives. Once you get further back into your own code, you can rule out the presence of any nulls if you want it that way and then you don’t have to worry about it anymore. Haskell supports this coding style directly in its type system, so it can give nice practice in it even if you only play around with Haskell.
Actually, maybe it would be neat to look at a brief example of this, just for kicks…@eska I think you might find this interesting, on the topic of your question, since Haskell is a quite different language from Python and kind of involves a different “view of the world.” Maybe this will address your question better than my earlier post—I kind of feel like I didn’t do the best job there. 
I’ll revisit my box-drawing example from above in Haskell-land, but with a bit of input-checking for illustrative purposes. Here’s the code; I’ll explain line-by-line afterwards. (I’m using a screenshot of my text editor because this forum’s syntax highlighter doesn’t seem to be configured to support Haskell, but here’s the file if you want to play around with it.)
% ghc box.hs
[1 of 1] Compiling Main ( box.hs, box.o )
Linking box ...
% ./box 5 3
*****
*****
*****
% ./box
Usage: box WIDTH HEIGHT
It could be fancier…like, it errors out with the message “box: Prelude.read: no parse” if you pass non-numbers which is slightly clunky…but I want to keep the code short ‘n’ sweet.
So, anyway, these imports
import System.Environment
import System.Exit
are for things like getArgs (to get command-line arguments) and exitFailure (to exit with a non-zero error code).
Next I declare a couple type synonyms:
type Dimension = Int
type Dimensions = (Dimension, Dimension)
This is so that, if I want to change the underlying type for these, I don’t have to do it all over the codebase. This might seem like overkill for a tiny example, but it actually came in handy, because I forgot at first that take requires an Int (hardware integer) as opposed to an Integer (arbitrary-precision integer) and I was using Integer for the box dimensions beforehand.
Anyway, then we have the actual box-drawing function.
rect :: Dimensions -> String
rect (w,h) =
let line = (take w $ repeat '*') ++ ['\n']
lines = take h (repeat line)
in concat lines
This makes a w-long list of asterisks with a newline appended, then makes a h-long list of those lists, then concatenates those lists together, yielding a single String. (In Haskell, String is a synonym for [Char].)
Note that this function, and the Dimension and Dimensions types, have nothing to do with IO. They are “pure”; they exist in an isolated world where we know already that we have actual integers for width and height. (We could actually do more in rect to ensure correctness, again, like check for negative numbers or 0, but you get the idea—the point is that it only makes sense as a function once you’ve already got an actual width and height in hand.)
Then we get into the impure code—the code that is concerned with IO. The design of this code is motivated by the fact that the user might not enter the command line arguments properly—conceivably the program might receive any or no text as input—and we want to make some effort to give them a good experience regardless.
parseArgs :: [String] -> IO Dimensions
parseArgs (inw:inh:[]) = do
let w = read inw :: Dimension
let h = read inh :: Dimension
return (w,h)
parseArgs _ = usage
usage = do
progn <- getProgName
putStrLn $ "Usage: " ++ progn ++ " WIDTH HEIGHT"
exitFailure
The idea here is that parseArgs expects the command-line arguments as a list of Strings. The first definition matches a list with exactly two strings, then tries to parse them as Dimensions and returns the result. The second catch-all definition prints a usage message to the console and exits with a failing error code.
Finally we have main:
main = do
dims <- getArgs >>= parseArgs
putStr $ rect dims
Haskell’s getArgs has the type IO [String], while >>= (the “bind” operator) takes the [String] result from getArgs (if it succeeds) and runs it through parseArgs, which “re-wraps” its result in IO. You can think of >>= as carrying out the argument parsing “within IO.” If the parsing succeeds, we “unwrap” the result with <- and store it in dims.
Then, we perform the pure conversion of dims to a box-of-asterisks String using rect dims, then pass the String to putStr to finish out the program.
So, you can kind of see that there’s this very clear demarcation between the “edge” of the program where things are uncertain and the “interior” where we know much better what’s going on and what value things might conceivably be and so on. Even in a more traditional imperative language that supports null and so on, you can still code in this style—check for invalid input (null or otherwise) at the edge of the program where I/O is taking place, and then in the interior you won’t have to worry about it, making your life easier.
As a side note, if you’re writing a library, I’m a firm believer in not worrying overmuch in the code itself about the user passing invalid input. Obviously like, worry about it to the extent that it could cause real harm, and try to give clear and instructive error messages when they’re needed, but beyond that, I think the best place to tell people how to use your API is in the documentation. I think there’s definitely a place for supplying totally dangerous, unchecked operations and just telling the user to be careful with them—that gives them the most flexibility when performance is critical. (You can supply a safer version too when that makes sense, like how C++ gives the bounds-checked at() as an alternative to C-style array subscripting.) If you spend too much time and energy protecting people from themselves, you can make your library needlessly awkward to use, too; you can’t really predict what people will need from it on some level, so I think it’s good not to constrain it more than you have to.
There’s nothing wrong with 1-based indexing! It’s only a convention after all. 0-based makes sense with C’s vision of the world where an array is just a pointer to the start of the array and you can do pointer arithmetic etc., but in mathematics it’s conventional to number the elements of a sequence starting from 1, so I think when you’re trying to represent something more with that character 1-indexing can be more intuitive. There’s almost no situations today where the performance aspect would matter, either.
i mean there’s literally something wrong with it in that the math is harder. that’s what my example was showing!!!
it’s not even about terseness – which i largely think is a negative virtue in programming – it’s that my code loses clarity because i’m having to add or subtract 1s all over the place.
it’s also pretty annoying when you’re trying to represent a 2d grid that you want to start at (0,0), because who the hell starts a coordinate grid at (1,1)? not to mention mapping 2d coordinates into an index for a 1d array (my standard way uses modulus, thus it has the same problem as my example above).
i have written multiple games in lua at this point, and i went in with your same attitude – that it’s just convention – but i have not had a single instance where it took fewer operations and less mental burden than 0-based indexing did. i’d love to hear a counter-example if you have one! when you need to use the index in computations, i can only think of examples where 1-based-indexing is worse.
So, sure, there definitely are cases where 0 is nicer, I’m not saying the decision is arbitrary—when I say it’s just a convention I just mean that there’s not, like, giant flaming letters in the sky forcing one or the other on you. I guess that and like, when you’re the one defining the interface, you can make the numbers mean whatever you want.
For starters, I guess I’ll say, if you have to add and subtract ones in a lot of places, I think it’s worth thinking about ways to abstract that work out in whatever context it’s happening in. Maybe that’s kind of obvious but I think it’s worth noting. Some languages give you more syntactic room to compensate for this than others—if you can redefine the array subscripting operator for a given type, for example, that may be very handy. Accessor functions will probably suffice if nothing else is available. In general, try to make the indexing behavior you want part of the interface of a type, and then use that type where you need that indexing behavior. I don’t know Lua very well so I’m not in a great position to give examples using it but that’s what I would try to do in basically any language.
That aside, I think 0-indexing is more sensible whenever you want to be able to treat some indices as offsets. 0 is the additive identity and naturally represents “an offset of nothing,” which you kind of have to have to make an environment for yourself where you can do additive calculations with offsets and have it work out. That’s basically what I was trying to get at with my C pointer arithmetic example, and it’s true with screen coordinates too and anything else of that nature. If you have the urge to think of your indices as ticks along a number line, or especially on the axes of a Cartesian grid, etc., 0-indexing will probably be nicer.
The most obvious place I can think of where I might consider 1-indexing is when I’m taking indices from the user and it’s easier for them to think in terms of 1-indexing. Actually, with Wumpus, that’s not a bad example, since the rooms in Wumpus are numbered 1–20. I think, for a lot of people, especially non-programmers, that just feels nicer and more intuitive than if the rooms were numbered 0–19. For the traditional text-based Wumpus interface, the user may actually be passing in “1” or “20” or whatever to signify rooms, so you save yourself a bit of work parsing their input and reporting room numbers to them if you use a 1-indexed room list—otherwise you have to do the same adding/subtracting rigamarole. It all depends on what you want to do with the indices.
EDIT: This is maybe a silly example, but if you only want to multiply the indices, 1 makes more sense as a “center value” than 0. That’s a rare case, though, obviously.
Also, sorry, I realize I should say, I actually thought you were taking the opposite position before…like that 1-indexing and 0-indexing are both good or w/e…I wasn’t paying enough attention to your code sample earlier so I apologize for that I thought I was agreeing with you at first. What I said just before does represent, like, my true opinion, but I wouldn’tve bothered saying anything about it if I had gotten where you were coming from initially. It does seem strange to me that arrays in Lua are 1-indexed—I think in practice the situations where you would specifically want 0-indexed arrays are probably more common in daily life (and definitely in graphical game development) than the situations where you would want 1-indexed arrays, so I see how it could be an awkward situation in that language.
I thought about this a bit further and I have something I think might be worth consideration. Oftentimes, when you really want to have a 0-indexed array specifically, I think what might be really nice, a lot of the time, is normalized 0.0–1.0 indexing. This might seem kind of like a strange point to make but I do think there’s something to it. You can set this up without much trouble in most any language.
I can think of two common styles of indexing like this I regularly use in my own life. One is one-dimensional normalized wraparound indexing, i.e. with 0.0 at the front, 1.0 at the back, and x == x + 1.0 == x - 1.0. You can get this in Ruby like this, for example (let me know if it would be better if I gave examples in a different language):
class NormArr < Array
def at(ndx)
self[((ndx % 1.0) * (size - 1)).round]
end
end
ns = NormArr.new((0..255).to_a)
ns.at(0.5)
#=> 128
ns.at(1.5)
#=> 128
ns.at(-0.5)
#=> 128
(0..3).map {|n| ns.at(2**-3 * n) }
#=> [0, 32, 64, 96]
This is really great if the array holds audio samples, a table you want to seek in with interpolation (as it’s written it’s using nearest-neighbor interpolation but you could do linear, cubic, etc. instead), anything like that. I use this style of interface all the time for all sorts of various random things. Csound has built-in support for this style of indexing in its table opcodes (table3 for cubic interpolation) with an ixmode and iwrap of 1.
(As a side note, although Ruby has 0-indexed arrays, if it had 1-indexed arrays, and you wanted to instead index over the range [1,size] instead of [0, size - 1], you would just have to do
# ...
def at(ndx)
self[((ndx % 1.0) * (size - 1)).round + 1]
end
# ...
instead, and then you wouldn’t have to think about it otherwise.)
Another setting like this I can think of is when I’m interfacing with a 2D image and I want normalized Cartesian coordinates, where (0.0, 0.0) is the center of the image, (-1.0, 1.0) is the top-left corner, (1.0, -1.0) is the bottom right corner, etc. Here I may or may not want wraparound. Often when I’m working with this kind of interface it’s in the context of a shader or the like; in Vulkan you have (0.0, 0.0) as the top-left corner and (1.0, 1.0) as the bottom-right, so in a GLSL fragment shader targeting Vulkan, if you’ve put the results of your Cartesian coordinate calculations in a vec2 called result:
vec2 fragpoint = result/vec2(2, -2) + vec2(0.5, 0.5);
(Note if you want to do this in a different language that GLSL vector multiplication/division is componentwise.) This is without wraparound, which I think I usually use more often, but if you did want wraparound you could do mod(fragpoint, 1.0) afterwards or that sort of thing.
If I was instead rendering an image from Ruby, which would generally involve (0, 0) as the top-left corner and (width - 1, height - 1) as the bottom-right corner, to give myself normalized Cartesian coordinates I might do e.g.:
require 'chunky_png'
require 'matrix'
def v(x, y)
Vector[x, y]
end
class Image
attr_reader :inner, :w, :h
def initialize(w, h)
@inner = ChunkyPNG::Image.new(w, h, ChunkyPNG::Color::TRANSPARENT)
@w = w
@h = h
fill(*([0.2, 1.0, 0.5].map { _1 / 8 } + [1.0]))
end
def []=(pnt,col)
res = (pnt.map2(v(2, -2), &:/) + v(0.5, 0.5))
.map2(v(w, h) - v(1,1)) { (_1 * _2).round }
@inner[*res.to_a] = chunky_col(*col)
end
def chunky_col(*col)
ChunkyPNG::Color.rgba(*col.map { (255 * _1).round })
end
def fill(*col)
(0...w).each do |x|
(0...h).each do |y|
@inner[x, y] = chunky_col(*col)
end
end
end
def save(fname)
@inner.save(fname)
end
end
include Math
TAU = 2*PI
@img = Image.new(3840, 2160)
TICKS = 2**21
def draw(a, b, c, d, e, f, g, h)
TICKS.times do |t|
dist = t.to_f / (TICKS - 1)
f = sin(dist*a*TAU + b)
g = cos(dist*c*TAU + d)
@img[v(f*g + f*0.9, f*g - g*0.8).map { _1 / 2 }] =
[
sin(dist*e*TAU),
cos(dist*f*TAU),
sin(dist*g*TAU),
cos(dist*h*TAU),
].map { _1/2 + 0.5}
end
end
args = [2960, 105, 1005, 3251, 165, 813, 1908, 3172]
draw(*args)
draw(*args.map { _1 / 7 })
@img.save('wrraurr.png')
original w/ transparency
EDIT: You know, I realize I overwrote the f and g arguments in draw but who cares I guess, it gives better results that way. You can tell that part of the code evolved very organically.
yeah i think working w/ shaders and pico8 sort of converted me to wanting to normalize more ranges from 0.0-1.0.
for pico8, all trig functions take an angle from 0-1 which i find preferable to radians since radians can give you inexact results for the angles i use most that i want to be very exact (90 degrees).
I might remember some of the CSS and HTML I learned so I could customize my Myspace page back in the day, and the C++ I wrote a calculator program in for a highschool class.
the idea of normalised indexing had never occurred to me and i literally do a lecture every year called “no number greater than one, no number less than negative one” which posits that 90% of game maths boils down to this range (it’s a lecture designed to get kids to be less afraid of mathematics by showing the links between different types of data/input/output and how if you understand one example you can almost certainly understand the rest).
i’m also realising that another use-case for normalised indexing is imposter sprites: converting a view-angle to an index (especially when working with single-axis imposters) is literally the entire trick!
Haha 
I’m really glad that could be useful to you! I’m not sure I would have thought of it without my experience using the musical programming environment Csound.
Csound makes heavy use of precomputed “lookup tables,” in the 1970s-ish sense of a 1D array holding the sampled output of some expensive function. It offers an interface to these tables where you can seek in them with nearest-neighbor, linear, or cubic interpolation, and that interface allows normalized 0–1 indexing with clamping or wraparound at the edges. This crops up a lot in Csound, so if you do a lot of Csound programming you end up getting very used to this idea. It’s just as useful in games as it is in audio synthesizers (I’m…not entirely sure what separates a game from an interactive synth honestly, except maybe the perspective of the player ).
Yeah, I mean, in a sense you can cram a lot of math at all into that range. XD Maybe this is exactly the point of your talk but um, I think a lot when doing game or audio programming about how any continuous function that is bounded above and below has a greatest lower bound and a least upper bound, and if you scale the function by the inverse of whichever of those is larger in magnitude, it will range over [-1, 1] or some continuous suberinterval of it containing 1 or -1. Also how like, because any continuous periodic function (including any continuous function over a finite interval, looped) can be approximated however far as a trigonometric series via Fourier analysis, and because if you have a finite trigonometric series it will always be bounded above and below and can thus be scaled into the range [-1, 1], trigonometric series provide a very rich expressive medium for constructing “knob-twiddling patterns” in any kind of artistic programming context. *deep breath* Those are some of my like, favorite things in programming.
Anyway. It’s cool that you would try to turn your students on to stuff like that! I hope some of them do get into it, I feel like those ideas become a fun playground if you’re receptive to them and have a computer available.
Yes, absolutely, and on the GPU it’s even cheap to interpolate between two of the frames! ^^
I had a section of “maybe I should do Computer Science” in college back in the Lower Paleozoic so the languages that I’ve worked in are: ANSI C, K&R C, and Intel/Motorola/MIPS RISC assembly. And a little Perl. I should really dip my toe back into something kind of modern.
You might like contemporary C++ ^^ C++17 is very widely supported now, and I think every program in K&R will compile with a C++17 compiler (if not it’s at least very close to). It feels kind of like, a lot of very serious people took everything you would write in C “aside from the main program logic” and made another language out of that.
Ruby has a kind of Perl-esque character, also—it has the same regex synax, basically, and supports things like $1 for the first capture group of the last regex match, among other things. The founder of the language, Matz, is a big Larry Wall fan. (Although, who it was really a big hit with initially was the Smalltalk crowd it seems like, because of the character of its OO facilities.)
Both C and Perl still have a huge presence in the world, of course—C especially but I think Perl 5 still runs on many web servers.
A long while ago I was between jobs, looking for technical writing jobs at job fairs and recruiters kept asking me specifically if I knew SQL and I still don’t know what was up with that.
That’s funny, I wonder what for 
I could believe there was a huge market for SQL books at that time, and probably today too…I get the impression that it’s a whole huge industry unto itself, basically, like database administration and so on. I don’t know if that’s actually what they would be hiring you to write about, though, I guess.
I love SQLite these days, just as a side note, I’m so glad I took some time to get properly familiar with it last year…I feel like the idea of relational databases honestly makes it feel a lot easier to think about how to program a game (or any complicated program that needs to process a lot of variegated input) in a way that will feel supple and flexible and easy to change etc., just because it puts such a strong emphasis on minimizing needless dependencies in how you arrange data.
Oh yeah—also, if you know the assembly language for your CPU (which you might at least partially if you have an x86-64 CPU since you studied Intel; it has some new instructions and random little differences from earlier Intel instruction sets but it doesn’t seem that different really from what I’ve seen) GCC can produce really nice Intel-syntax annotated assembly from C++ code if you use the flags -S -masm=intel, and GDB can step through your code instruction-by-instruction and show you the contents of all the CPU registers while it does this and things. Just like with C, this can really help you both better understand the language and compiler, help you spot optimization opportunities, ensure that code you want to be vectorized is actually getting vectorized, etc., so it’s definitely a skill you can benefit from with C++.
1to5.cpp:
#include <iostream>
int main()
{
for (auto i = 1; i <= 5; ++i) {
std::cout << i << '\n';
}
}
// prints:
//
// 1
// 2
// 3
// 4
// 5
g++ -S -masm=intel 1to5.cpp:
.file "1to5.cpp"
.intel_syntax noprefix
.text
#APP
.globl _ZSt21ios_base_library_initv
#NO_APP
.globl main
.type main, @function
main:
.LFB1983:
.cfi_startproc
push rbp
.cfi_def_cfa_offset 16
.cfi_offset 6, -16
mov rbp, rsp
.cfi_def_cfa_register 6
sub rsp, 16
mov DWORD PTR -4[rbp], 1
jmp .L2
.L3:
mov eax, DWORD PTR -4[rbp]
mov esi, eax
lea rax, _ZSt4cout[rip]
mov rdi, rax
call _ZNSolsEi@PLT
mov esi, 10
mov rdi, rax
call _ZStlsISt11char_traitsIcEERSt13basic_ostreamIcT_ES5_c@PLT
add DWORD PTR -4[rbp], 1
.L2:
cmp DWORD PTR -4[rbp], 5
jle .L3
mov eax, 0
leave
.cfi_def_cfa 7, 8
ret
.cfi_endproc
.LFE1983:
.size main, .-main
.section .rodata
.type _ZNSt8__detail30__integer_to_chars_is_unsignedIjEE, @object
.size _ZNSt8__detail30__integer_to_chars_is_unsignedIjEE, 1
_ZNSt8__detail30__integer_to_chars_is_unsignedIjEE:
.byte 1
.type _ZNSt8__detail30__integer_to_chars_is_unsignedImEE, @object
.size _ZNSt8__detail30__integer_to_chars_is_unsignedImEE, 1
_ZNSt8__detail30__integer_to_chars_is_unsignedImEE:
.byte 1
.type _ZNSt8__detail30__integer_to_chars_is_unsignedIyEE, @object
.size _ZNSt8__detail30__integer_to_chars_is_unsignedIyEE, 1
_ZNSt8__detail30__integer_to_chars_is_unsignedIyEE:
.byte 1
.ident "GCC: (Gentoo 13.2.1_p20240210 p14) 13.2.1 20240210"
.section .note.GNU-stack,"",@progbits
One thing you can see easily here is C++'s classic name mangling, which, if you haven’t heard of it before, is where the compiler adds a bunch of implementation-specific characters to function names to facilitate things like overloading (as opposed to C, you can define different functions with the same name in C++ as long as they take different types of arguments). Another thing you can see is that it returns 0 from main() even though I didn’t actually write a return statement, which is allowed in C++ and also in C99 (although of course in real production code it’s likely you would want to return a meaningful status).
Here’s an example of something the compiler can vectorize, while also demonstrating a wider variety of C++ features. We pick a basic integer type, then have the compiler multiply the largest number of integers of that type as it can simultaneously using a single SIMD instruction, given the available features on the host (assuming x86) CPU (note that this code is also slightly GCC-specific; it will work with Clang but I think probably not MSVC…Windows users, note that you can use GCC on Windows to compile Windows-native binaries using the wonderful free software MSYS2):
vec.cpp:
#include <array>
#include <random>
#include <functional>
#include <iostream>
#include <ctime>
#include <limits>
#include <climits>
#include <cxxabi.h>
int main()
{
using std::size_t;
using std::array;
// our integer type
#ifndef NUM_W
#define NUM_W short
#endif
typedef unsigned NUM_W num;
constexpr size_t num_bits = sizeof(num) * CHAR_BIT;
#if defined __AVX512__
#define SIMD_SZ 512
#elif defined __AVX2__
#define SIMD_SZ 256
#elif defined __SSE2__
#define SIMD_SZ 128
#elif defined __MMX__
#define SIMD_SZ 64
#else
#define SIMD_SZ sizeof(num)
#endif
constexpr size_t num_cnt = SIMD_SZ / num_bits;
typedef array<num, num_cnt> col;
col b;
col c;
using std::numeric_limits;
using std::default_random_engine;
using std::uniform_int_distribution;
using std::bind;
constexpr num max_rand_val = numeric_limits<num>::max()
>> num_bits/2;
default_random_engine gen(time(nullptr));
uniform_int_distribution<num> dist(1, max_rand_val);
auto roll = bind(dist, gen);
for (col::size_type i = 0; i < num_cnt; ++i) {
b[i] = roll();
c[i] = roll();
}
col a;
// the compiler can vectorize this
for (col::size_type i = 0; i < num_cnt; ++i) {
a[i] = b[i] * c[i];
}
int dm_status;
const char* num_t_name = abi::__cxa_demangle(typeid(num).name(),
nullptr,
nullptr,
&dm_status);
if (dm_status) {
num_t_name = "integer";
}
using std::cout;
cout << "multiplying " << num_cnt << " " << num_t_name;
if (num_cnt != 1) { cout << "s simultaneously"; }
cout << ":\n";
for (auto&& i : a) {
std::cout << i << '\n';
}
}
As a side note, in order to actually have the compiler use the SIMD registers, we need to fill the source arrays at runtime (hence the random numbers). If we fill them using values known at compile time, GCC is smart enough to just peform the multiplications during compilation instead.
Compiling this on my system with -O2 for typical optimizations, -ftree-vectorize for auto-vectorization, and -march=native to use the host CPU’s full instruction set (these are actually the flags I use to build Gentoo packages in my environment during install):
% g++ -O2 -ftree-vectorize -march=native vec.cpp -o vec
% ./vec
multiplying 16 unsigned shorts simultaneously:
4464
13561
1308
51000
3040
13052
8246
26520
58320
14734
30690
1760
1440
678
9129
26108
(Note that a binary built with -march=native is not necessarily portable—by “host” I mean the system hosting the compiler.)
Anyway, my CPU supports AVX2, hence this result. We can see this in more detail by examing the asm:
.file "vec.cpp"
.intel_syntax noprefix
.text
#APP
.globl _ZSt21ios_base_library_initv
#NO_APP
.align 2
.p2align 4
.type _ZNSt24uniform_int_distributionItEclISt26linear_congruential_engineImLm16807ELm0ELm2147483647EEEEtRT_RKNS0_10param_typeE.isra.0, @function
_ZNSt24uniform_int_distributionItEclISt26linear_congruential_engineImLm16807ELm0ELm2147483647EEEEtRT_RKNS0_10param_typeE.isra.0:
.LFB5920:
.cfi_startproc
push r14
.cfi_def_cfa_offset 16
.cfi_offset 14, -16
movzx eax, si
movzx r14d, dx
sub r14, rax
push r13
.cfi_def_cfa_offset 24
.cfi_offset 13, -24
mov r13, rdi
push r12
.cfi_def_cfa_offset 32
.cfi_offset 12, -32
mov r12, rax
push rbp
.cfi_def_cfa_offset 40
.cfi_offset 6, -40
push rbx
.cfi_def_cfa_offset 48
.cfi_offset 3, -48
cmp r14, 2147483644
ja .L2
lea rdi, 1[r14]
mov eax, 2147483645
xor edx, edx
movabs r8, 8589934597
div rdi
mov rdx, QWORD PTR 0[r13]
imul rdi, rax
mov r9, rax
.p2align 4,,10
.p2align 3
.L3:
imul rsi, rdx, 16807
mov rax, rsi
mov rcx, rsi
mul r8
sub rcx, rdx
shr rcx
add rdx, rcx
shr rdx, 30
mov rcx, rdx
sal rcx, 31
sub rcx, rdx
sub rsi, rcx
lea rax, -1[rsi]
mov rdx, rsi
cmp rax, rdi
jnb .L3
xor edx, edx
mov QWORD PTR 0[r13], rsi
div r9
pop rbx
.cfi_remember_state
.cfi_def_cfa_offset 40
pop rbp
.cfi_def_cfa_offset 32
add eax, r12d
pop r12
.cfi_def_cfa_offset 24
pop r13
.cfi_def_cfa_offset 16
pop r14
.cfi_def_cfa_offset 8
ret
.p2align 4,,10
.p2align 3
.L2:
.cfi_restore_state
mov rdx, r14
movabs rax, -9223372028264841207
movabs rbp, 8589934597
shr rdx
mul rdx
shr rdx, 29
mov ebx, edx
.L9:
xor esi, esi
mov edx, ebx
mov rdi, r13
call _ZNSt24uniform_int_distributionItEclISt26linear_congruential_engineImLm16807ELm0ELm2147483647EEEEtRT_RKNS0_10param_typeE.isra.0
imul rsi, QWORD PTR 0[r13], 16807
mov ecx, eax
mov rax, rsi
mul rbp
mov rax, rsi
sub rax, rdx
shr rax
add rdx, rax
shr rdx, 30
mov rax, rdx
sal rax, 31
sub rax, rdx
sub rsi, rax
movzx eax, cx
imul rax, rax, 2147483646
mov rdx, rsi
mov QWORD PTR 0[r13], rsi
dec rdx
add rax, rdx
setc dl
movzx edx, dl
cmp r14, rax
jb .L9
test rdx, rdx
jne .L9
pop rbx
.cfi_def_cfa_offset 40
add eax, r12d
pop rbp
.cfi_def_cfa_offset 32
pop r12
.cfi_def_cfa_offset 24
pop r13
.cfi_def_cfa_offset 16
pop r14
.cfi_def_cfa_offset 8
ret
.cfi_endproc
.LFE5920:
.size _ZNSt24uniform_int_distributionItEclISt26linear_congruential_engineImLm16807ELm0ELm2147483647EEEEtRT_RKNS0_10param_typeE.isra.0, .-_ZNSt24uniform_int_distributionItEclISt26linear_congruential_engineImLm16807ELm0ELm2147483647EEEEtRT_RKNS0_10param_typeE.isra.0
.section .rodata.str1.1,"aMS",@progbits,1
.LC0:
.string "integer"
.LC2:
.string "multiplying "
.LC3:
.string " "
.LC4:
.string "s simultaneously"
.LC5:
.string ":\n"
.section .text.startup,"ax",@progbits
.p2align 4
.globl main
.type main, @function
main:
.LFB5152:
.cfi_startproc
push rbp
.cfi_def_cfa_offset 16
.cfi_offset 6, -16
xor edi, edi
mov rbp, rsp
.cfi_def_cfa_register 6
push r14
push r13
push r12
push rbx
and rsp, -32
sub rsp, 160
.cfi_offset 14, -24
.cfi_offset 13, -32
.cfi_offset 12, -40
.cfi_offset 3, -48
mov rax, QWORD PTR fs:40
mov QWORD PTR 152[rsp], rax
xor eax, eax
lea r12, 32[rsp]
lea rbx, 64[rsp]
call time@PLT
mov DWORD PTR 16[rsp], 16711681
lea r11, 24[rsp]
mov rcx, rax
movabs rax, 8589934597
mul rcx
mov rax, rcx
sub rax, rdx
shr rax
add rdx, rax
shr rdx, 30
mov rax, rdx
sal rax, 31
sub rax, rdx
sub rcx, rax
mov eax, 1
cmove rcx, rax
xor r10d, r10d
mov QWORD PTR 24[rsp], rcx
.p2align 4,,10
.p2align 3
.L13:
mov edx, 255
mov esi, 1
mov rdi, r11
call _ZNSt24uniform_int_distributionItEclISt26linear_congruential_engineImLm16807ELm0ELm2147483647EEEEtRT_RKNS0_10param_typeE.isra.0
mov edx, 255
mov esi, 1
mov rdi, r11
mov WORD PTR [r12+r10*2], ax
call _ZNSt24uniform_int_distributionItEclISt26linear_congruential_engineImLm16807ELm0ELm2147483647EEEEtRT_RKNS0_10param_typeE.isra.0
mov WORD PTR [rbx+r10*2], ax
inc r10
cmp r10, 16
jne .L13
mov rdi, QWORD PTR _ZTIt[rip+8]
vmovdqa ymm1, YMMWORD PTR 32[rsp]
xor eax, eax
lea rcx, 12[rsp]
lea r12, _ZSt4cout[rip]
lea r13, 128[rsp]
cmp BYTE PTR [rdi], 42
vpmullw ymm0, ymm1, YMMWORD PTR 64[rsp]
vmovdqa YMMWORD PTR 96[rsp], ymm0
lea r14, 11[rsp]
sete al
xor edx, edx
xor esi, esi
add rdi, rax
vzeroupper
call __cxa_demangle@PLT
lea rsi, .LC2[rip]
mov rdi, r12
mov rbx, rax
mov eax, DWORD PTR 12[rsp]
test eax, eax
lea rax, .LC0[rip]
cmovne rbx, rax
call _ZStlsISt11char_traitsIcEERSt13basic_ostreamIcT_ES5_PKc@PLT
mov esi, 16
mov rdi, rax
call _ZNSo9_M_insertImEERSoT_@PLT
lea rsi, .LC3[rip]
mov rdi, rax
call _ZStlsISt11char_traitsIcEERSt13basic_ostreamIcT_ES5_PKc@PLT
mov rsi, rbx
lea rbx, 96[rsp]
mov rdi, rax
call _ZStlsISt11char_traitsIcEERSt13basic_ostreamIcT_ES5_PKc@PLT
lea rsi, .LC4[rip]
mov rdi, r12
call _ZStlsISt11char_traitsIcEERSt13basic_ostreamIcT_ES5_PKc@PLT
lea rsi, .LC5[rip]
mov rdi, r12
call _ZStlsISt11char_traitsIcEERSt13basic_ostreamIcT_ES5_PKc@PLT
jmp .L18
.p2align 4,,10
.p2align 3
.L25:
mov edx, 1
mov rsi, r14
add rbx, 2
call _ZSt16__ostream_insertIcSt11char_traitsIcEERSt13basic_ostreamIT_T0_ES6_PKS3_l@PLT
cmp rbx, r13
je .L24
.L18:
movzx esi, WORD PTR [rbx]
mov rdi, r12
call _ZNSo9_M_insertImEERSoT_@PLT
mov BYTE PTR 11[rsp], 10
mov rdi, rax
mov rax, QWORD PTR [rax]
mov rax, QWORD PTR -24[rax]
cmp QWORD PTR 16[rdi+rax], 0
jne .L25
mov esi, 10
add rbx, 2
call _ZNSo3putEc@PLT
cmp rbx, r13
jne .L18
.L24:
mov rax, QWORD PTR 152[rsp]
sub rax, QWORD PTR fs:40
jne .L26
lea rsp, -32[rbp]
xor eax, eax
pop rbx
pop r12
pop r13
pop r14
pop rbp
.cfi_remember_state
.cfi_def_cfa 7, 8
ret
.L26:
.cfi_restore_state
call __stack_chk_fail@PLT
.cfi_endproc
.LFE5152:
.size main, .-main
.ident "GCC: (Gentoo 13.2.1_p20240210 p14) 13.2.1 20240210"
.section .note.GNU-stack,"",@progbits
You can see that much of the program is just the pseudorandom number generation and also that—and I think this is kind of interesting—it uses vmovdqa to pack b’s integers into the AVX register ymm1, then uses vpmullw to multiply them simultaneously with c’s integers on the stack and store the results in ymm0, after it which moves the results from ymm0 to the stack.
vmovdqa ymm1, YMMWORD PTR 32[rsp]
# ...
vpmullw ymm0, ymm1, YMMWORD PTR 64[rsp]
vmovdqa YMMWORD PTR 96[rsp], ymm0
I would think it would be faster to put them both in registers first since the instruction supports that, but I guess it must not be in this case. Anyway a YMMWORD is 256 bits so we fill the whole YMM register from the stack, and there’s no loop around the AVX instructions so we know we’re doing all the multiplications in one go; in other words, the program works as intended.
Let’s see what happens if we target plain AVX instead, using -march=sandybridge:
% g++ -march=sandybridge -O2 -ftree-vectorize vec.cpp -o vec_sandy
% ./vec_sandy
multiplying 8 unsigned shorts simultaneously:
97
19292
5249
4608
21516
3210
11356
11999
Here’s the vectorized multiplication:
vmovdqa xmm1, XMMWORD PTR 32[rsp]
vpmullw xmm0, xmm1, XMMWORD PTR 48[rsp]
vmovdqa XMMWORD PTR 64[rsp], xmm0
This uses the AVX vpmullw, which uses the 128-bit XMM registers instead. If we instead try to store 256 bits’ worth of integers on AVX, like by doing
#elif defined __AVX__
#define SIMD_SZ 256
then we instead get two multiplications, because AVX doesn’t have the wider vpmullw that AVX2 introduced:
vmovdqa xmm1, XMMWORD PTR 32[rsp]
vpmullw xmm0, xmm1, XMMWORD PTR 64[rsp]
vmovdqa XMMWORD PTR 96[rsp], xmm0
# ...
vmovdqa xmm2, XMMWORD PTR 48[rsp]
vpmullw xmm0, xmm2, XMMWORD PTR 80[rsp]
vmovdqa XMMWORD PTR 112[rsp], xmm0
Hence the limitation of 128 bits on AVX.
Here’s what happens if we do unsigned ints on AVX instead, by setting -DNUM_W=int:
% g++ -march=sandybridge -O2 -ftree-vectorize -DNUM_W=int vec.cpp -o vec_sandy_int
% ./vec_sandy_int
multiplying 4 unsigned ints simultaneously:
3842292
194173730
146962731
738989900
This works almost identically as before, except that it uses vpmulld (d for “doubleword”) instead of vpmullw:
vmovdqa xmm1, XMMWORD PTR 32[rsp]
vpmulld xmm0, xmm1, XMMWORD PTR 48[rsp]
vmovdqa XMMWORD PTR 64[rsp], xmm0
And with my AVX2 CPU:
% g++ -march=native -O2 -ftree-vectorize -DNUM_W=int vec.cpp -o vec_int
% ./vec_int
multiplying 8 unsigned ints simultaneously:
26275271
1834613172
3767632497
257349818
367152876
42965259
483179004
3308367740
vmovdqa ymm1, YMMWORD PTR 32[rsp]
# ...
vpmulld ymm0, ymm1, YMMWORD PTR 64[rsp]
vmovdqa YMMWORD PTR 96[rsp], ymm0
As one last little demonstration, if we compile the binary also with the flag -ggdb to add debug annotations, we can step through it with GDB like I mentioned at the outset:
% g++ -march=native -O2 -ftree-vectorize -DNUM_W=int -ggdb vec.cpp -o vec_int
% gdb ./vec_int
Then at the GDB prompt, if we enter
(gdb) tui enable
(gdb) layout asm
we can scroll around in the window showing the asm, find where the vectorized multiplication happens, and set a breakpoint there:
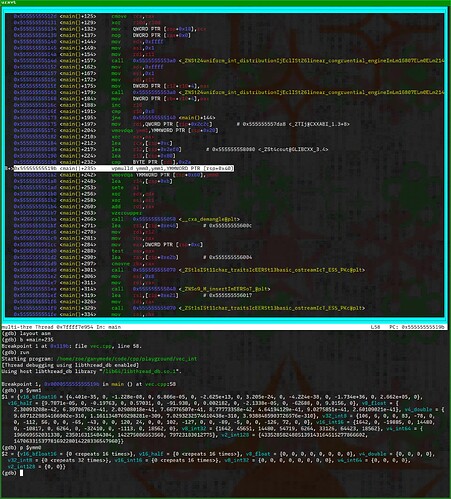
Then we can run the program and it will stop at that breakpoint, allowing us to examine the YMM registers:
You can see that ymm1 is filled with 8 random integers (v8_int32 is the right view on the register) and ymm0 is yet to be filled. If we step the code forward one instruction with stepi, we can see the multiplication results:
As a side note, when you’re doing more “normal” programming than this, GDB can also show you the contents of the CPU registers as you’re stepping through your code if you enter e.g. tui reg all for all the registers:
This isn’t quite as convenient for the vector registers specifically because their printout can go off the screen. The GDB docs say you should be able to scroll right and left too but it doesn’t seem to work for me in this window:
If you have this problem too, at least you can still view them using p.
Anyway, so, all of that is to say, if you like low-level programming, you can have a lot of fun with your CPU, C++, GCC, and GDB. 
You say that like it dates you but I was in college from 2015 to 2019 and after an intro class in Java my CS(E) degree was taught almost entirely with ANSI C and MIPS assembly.
yeah that right there is a big part of why is why I don’t have a CS degree, because I did not have the patience for any of that
I’m assuming that some departments must exist that teach CS the way it is generally practiced in industry now but I really have no idea how many, everyone who was going to college at the same time as I was (2006) for engineering was mostly seeking out capital-E engineering opportunities so it was more understandable that they’d have to suffer through java